社区项目开发数据库准备工作
本文共 253 字，大约阅读时间需要 1 分钟。
首先需要创建一个数据库，并建表导入数据，为后续操作做准备，这一步通常比较繁琐，但在实际项目开发中，除了DBA外，一般很少由开发人员建表
下面是简单的SQL语句
SHOW DATABASES;CREATE DATABASE community;SHOW DATABASES;USE community;SHOW TABLES;
表的创建和数据的导入，使用了外面的两个SQL脚本
数据库由以下几张表构成
其中user用户表的信息如下
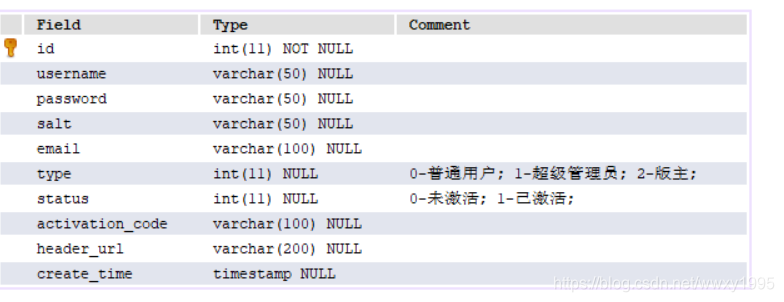
消息表如下
下一步，配置MyBatts，完成利用Java代码高效的操作数据库
转载地址：http://bfmv.baihongyu.com/
你可能感兴趣的文章
mysql安装和启动命令小结
查看>>
Mysql安装教程（命令行）
查看>>
mysql安装版安装
查看>>
MySQL安装配置教程(非常详细)，从零基础入门到精通，看完这一篇就够了
查看>>
mysql安装配置简介
查看>>
MySQL定义和变量赋值
查看>>
mysql定时任务事件清理单表数据
查看>>
MySQL定时器Events
查看>>
Mysql定时备份脚本
查看>>
mysql实战01|基础架构：一条SQL查询语句是如何执行的?
查看>>
Mysql实战之数据备份
查看>>
MySQL实战教程：从小白到大神的进阶之路！
查看>>
mysql实现成绩排名
查看>>
Mysql客户端中文乱码问题解决
查看>>
mysql客户端工具使用
查看>>
MySQL密码忘记，怎么办？
查看>>
mysql对同一张表进行查询和赋值更新
查看>>
mysql导入数据库出现:Incorrect string value: '\xE7\x82\xB9\xE9\x92\x9F' for column 'chinese' at row 1...
查看>>
mysql导入（ibd文件）
查看>>
Mysql工作笔记006---Mysql服务器磁盘爆满了_java.sql.SQLException: Error writing file ‘tmp/MYfXO41p‘
查看>>